HERE I AM NOW TRYING IN A PRACTICAL WAY. 

An imagined planet in its orbit around the sun.

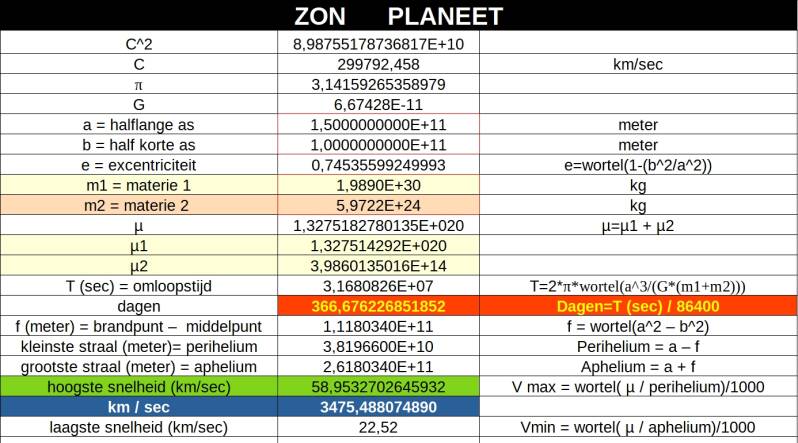
Here are the main details of the planet's orbit.

And yes " the matter is a product created by action of gravitation (µ) on light energy (E).

m1 = the matter of the sun , which here is equal to the mass M1.

            The sun also has a velocity but , I consider the planet and the sun in their mutual influence.

m2 = the matter of the planet , which because of the planet's velocity

             is not equal to the mass M2 .

µ = µ1 + µ2 , µ1 planet µ2 sun.

µ1 = m1* G. 

With the resources we now have we can calculate the total orbital period of the planet.

We can also calculate the smallest radius (perihelion ) and the largest radius (aphelion ).

With this we can now calculate the greatest velocity and the smallest velocity.

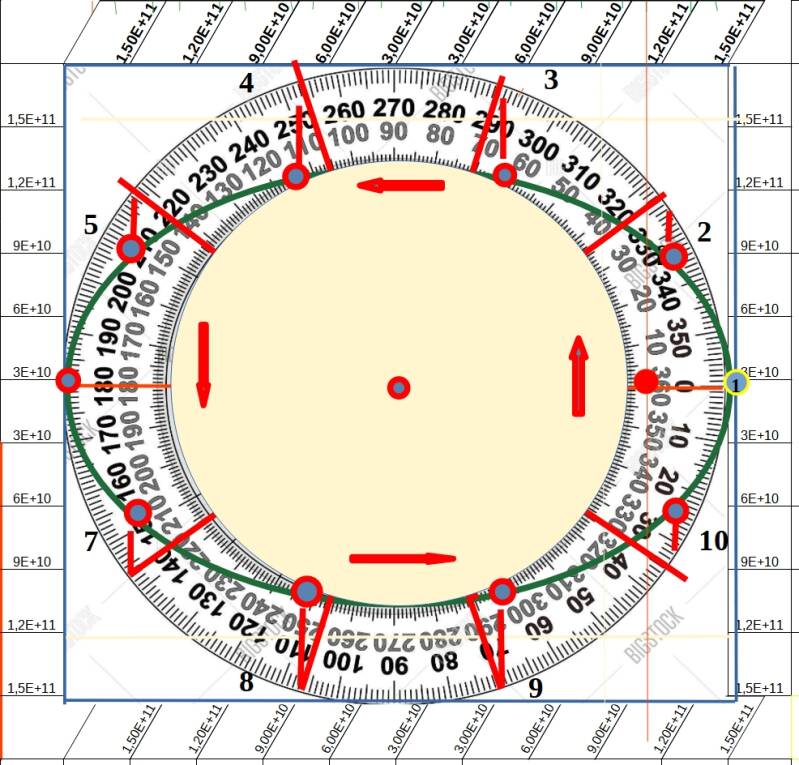
The green ellipse is the planetary orbit, showing 10 phases of the planet.

Phase 1 is the perihelion , phase 6 is the aphelion.

To the right of the ellipse the red dot is the location of the sun.

What I said about matter I am now going to apply to the orbit of a planet around the sun.

To explain this I must make the difference between matter and mass.

Matter is the energy that does not contribute to the motion.

Mass is the energy that represents both matter and motion.

If there is no motion , then the mass is equal to the matter.

So with anything that has a velocity there is a difference in mass and matter.

Matter represents the gravitation.

To clarify this I use the thermals Em and µm .

These two are always equal in matter.

If Em2 has a surplus then this manifests itself in movement of the planet.

The planet in my example has the highest velocity because it is in perihelion.

To get the energy needed for that speed, I make a detour and add to E1 an arbitrary amount of

energy E1+ . This energy is responsible for a certain speed.

By taking the ratio of the orbital velocity and the velocity calculated here, we can calculate the energy that is

is needed for the orbital speed.

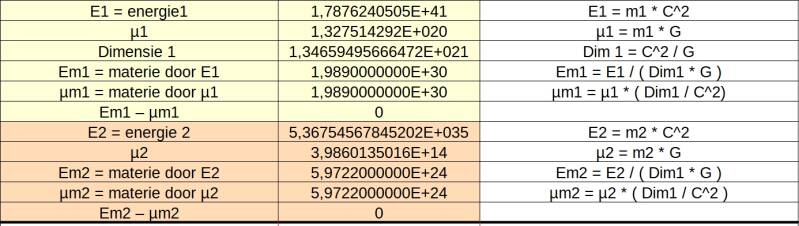
E2 =the energy of the planet.

Em2 =the matter that can be generated by E2. (planet)

µm2 = the matter that can be excited by µ2.  (planet)

If both of these are equal that they generate an amount of matter with no surplus.

Here Em1 = µm1.The matter of the sun is equal to 1.989E+30

Here Em2 = µm2 .The matter of the planet is equal to 5.9722E+24.

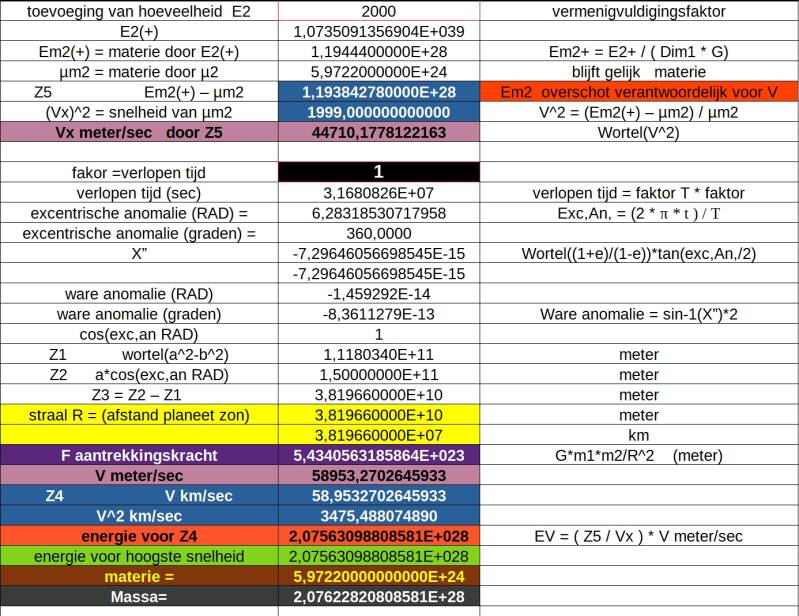
Now to cause a movement I am going to supply E2 with more energy. (energy of the planet)

I am now going to apply a random increment and multiply E2 by 2000.

A motion is now generated because Em2 and µm2 are no longer equal.

E2+ is the energy of the planet after adding. = 1.0735....E+39.

This allows Em2+ to generate more matter if µm2 also contains more energy.

But µm2 has remained the same so there is not more matter that can be generated

but there is now a surplus of energy which causes motion.

The whole thing happens in Dim1 because everything happens in the same solar system.

Dim1 = 1.34659495666472E+21.

Em2+ = 1.19444E+28

µm2 = 5.9722E+24

The difference is 1.19384E+28 is the energy required to generate V = 44710.18 m/sec.

In my example, I take the elapsed time = T ( one full orbit) = 1

The eccentric anomaly is 6.2832853...Radians or 360 degrees.

The true anomaly = -1.459292E-14 Rad .

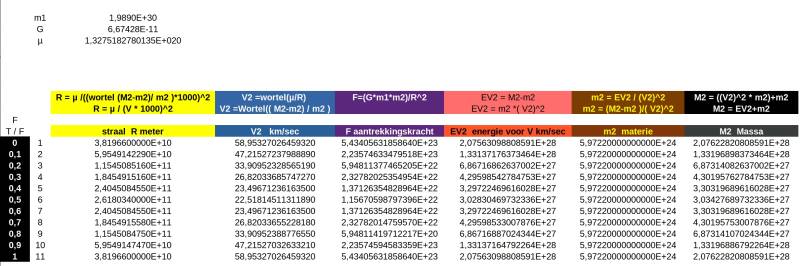
In the example below , the distance planet- sun ( R radius ) can then be calculated.

Similarly the force of attraction , velocity , Matter and mass.

Speed at this point is 58.95 km/sec.

Since we know that for 44710.18 m/sec an energy of 1.19384E+28 is needed, 

we can calculate the energy for speed 58.95 km/hr. (Do convert to km/sec).

I have thus divided the circulation into 10 . 

0.1 0.2 0.3 etc times the total orbit.

At 0 the radius is shortest (perihelion) , velocity = 58.95 km/sec , force of attraction is greatest ,

matter = 5.9722E+24 , mass = 2.076228..E+28 , etc.

So the Mass = matter * v^2

V = wortel( Mass / matter )

F= G * (matter1 * matter2) / R^2

 

Review the results of matter and Mass vs. velocity.